考研自划线什么时候出

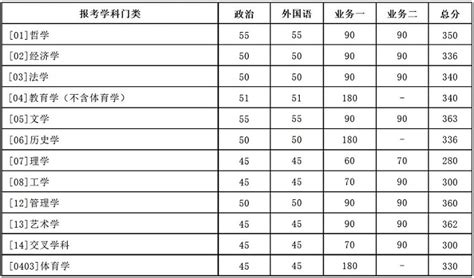
考研数学中的“木棍划线”问题

在考研数学中，有一类叫做“木棍划线”（也被称为“割圆术”）的问题，其解题方法和思路颇为独特。下面我们就来详细讲解一下。

1. 问题描述

假设有 $n$ 根木棍，长度分别为 $l_1, l_2, ..., l_n$，现在需要将这些木棍划分成 $m$ 段，使得每一段的长度相等，且最大，且该长度尽可能大。

2. 解题方法

我们根据题目要求，可以列出如下公式：

$$

\frac{l_1}{x} \frac{l_2}{x} ... \frac{l_n}{x}=m

$$

其中，$x$ 代表每一段的长度。观察上述公式，我们不难发现，这是一个关于 $x$ 的函数，在坐标系中可以表示出它的图像。

在这张图像中，我们需要找到满足 $m$ 的根号个数（根号的位置即图像与 $x$ 轴相交的点）。

而根据函数的不同情况，我们需要分别处理：

① 当函数为单峰函数时，只需找到函数最高点，则该点下方的图像与 $x$ 轴相交的点即所求。

② 当函数为一次函数时，其图像为一条直线，则从函数图像的左侧和右侧开始二分搜索，最后相交的两个点的中点即为所求。

③ 当函数为多峰函数时，则需要将其拆分为多个单峰函数和一条一次函数，然后分别处理。

3. 注意事项

1. 在进行二分搜索时，需要考虑精度误差。此时，我们可以采用如下方式：

先设定一个误差范围 $\epsilon$，然后在相交的两个点距离小于 $\epsilon$ 时，直接返回中点。

2. 在尝试求解校招、笔试、面试等题目时，请首先判断这是否为一道“木棍划线”问题，然后再采用相应的解题方法。

4. 总结

“木棍划线”问题需要我们具备对于函数图像和二分搜索的掌握。掌握好了这个问题的解题方法，相信在考研数学中，你也会游刃有余了。